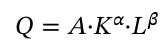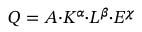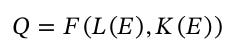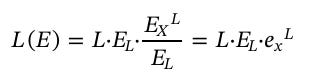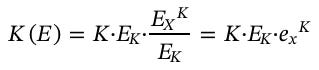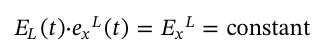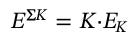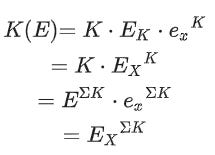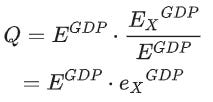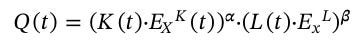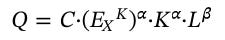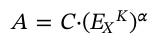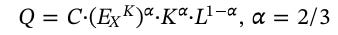Toplam Faktör Verimliliği (TFP) Gerçekte Nedir?

Enerji-temelli Cobb-Douglas üretim fonksiyonu

Bu yazıda neoklasik iktisatçıların kullandığı Cobb-Douglas üretim fonksiyonunu (CDPF) ekolojik iktisadın üretimin nasıl gerçekleştiğine yönelik sahip olduğu çok daha gerçekçi bakış açışı ile yeniden türeteceğiz.

Neoklasik iktisatta kullanıldığı şekliyle CDPF şu şekildedir.

Q, ekonomik çıktıdır. A, toplam faktör verimliliği. K, sermaye ve L, emektir. Sabit getiri (constant returns to scale) varsayımı altında K ve L’nin eksponentlerinin toplamı 1’e eşittir: α + β = 1. CDPF basitçe üretimin sermaye ve emeğe bağlı olduğunu söylemektedir.

Cobb-Douglas üretim fonksiyonuyla ilgili ciddi teorik ve empirik problemler bulunmakta fakat bunları bir kenara bırakarak spesifik bir problemle ilgileneceğiz: doğal kaynakların ve enerjinin denklemde yerinin olmaması. Neoklasik iktisatçılar hariç herkesin bildiği üzere üretim ekosistemden elde edilen hammaddelerin ve enerjinin kullanıldığı fiziksel bir süreçtir. Esasen ilk ortaya atıldığında fonksiyona doğal kaynak ve enerjinin eklenmesi gerektiği vurgulanmıştı fakat neoklasik iktisatçılar bunu umursamadan devam etmeyi tercih ettiler. Fonksiyona enerjiyi eklediğimizde şu hale gelir:

Sabit getiri varsayımı nedeniyle; α + β + χ = 1.

Burada kritik problem enerjinin eksponentinin kaç olduğudur. Neoklasik iktisatçılar eksponentleri belirleme işini girdilerin GDP içindeki harcama paylarına bakarak yaparlar. Bu yöntemdeki problem α ve β toplamının 1’e yakın olmasıdır. Enerjinin eksponenti ise 0.07 gibi oldukça düşük kalmaktadır. Bunun anlamı enerjinin üretimde hemen hemen hiçbir rol oynamadığıdır. Örneğin, enerji girdisindeki %10’luk bir düşüş ekonomik çıktıda %0.7 düşüşe yol açardı. Neoklasik iktisatçıların olmasa da normal insanların sezgileri bize enerjinin çok önemli ve yeri doldurulamaz bir rolü olduğunu söylemektedir. Yukarıda belirttiğimiz gibi üretim süreci ekosistemden elde edilen materyallerin enerji kullanılarak dönüştürülemesinden ibarettir. Empirik veriler gerçekten enerjinin çok daha büyük bir rol oynadığını kanıtlamaktadır. Örneğin, petrol tüketimindeki %10’luk bir düşüş GDP’nin normalde olacağına kıyasla yaklaşık %4 düşmesiyle sonuçlanır (Ayres ve Warr, 2009).

Yukarıdaki gösterim biçimiyle ilgili problem enerjinin, emek ve sermayenin ayrılmaz bir parçası olmasıdır. Yukarıdaki denklem ise enerjiyi bağımsız bir girdi olarak ele almaktadır. Gerçekte enerjiyi üretim sürecine fonksiyonun ima ettiği şekilde sokmak üretime değil yıkıma yol açardı. Gerçek dünyada emek ve sermaye enerjiyi kullanarak çalışmaktadır. “Enerji olmadan emek bir cesettir, enerji olmadan sermaye de bir heykel” (Keen ve ark., 2019). Dolayısıyla Q = F(L, K, E) şeklindeki bir fonksiyonel form yerine şu fonksiyonel formu elde etmeye uğraşmalıyız:

Bu fonksiyonel formun söylediği şey enerjinin, iş yapabilmek için emek ve sermaye tarafından yönlendirildiğidir. Diğer bir ifadeyle, eğer emek ve sermayeye enerji girdisi sıfır olsaydı emek ve sermaye iş yapamazdı. Somut olarak örnek vermek gerekirse eğer gıdalardan elde edilen metabolik enerji olmasaydı emek, iş yapamazdı çünkü ölmüş olurdu.

Daha teknik ifadelerle emek ve sermaye enerjiyi kullanışlı işe dönüştürmenin araçlarıdır. L(E) ve K(E) fonksiyonlarının girdisi enerji ve çıktısı kullanışlı iş potensiyelidir (ekserji). Tarif ettiğimiz fonksiyonlar matematiksel olarak şu şekilde gösterilir:

E_L ve E_K yıllık işçi başına ve “temsili makine” başına toplam enerji tüketimini ifade eder. e_x^L ve e_x^K enerji girdilerinin ekserjiye (kullanışlı iş potansiyeli) çevrilme verimliliğini ifade eder.

Sebeplerine girmeden basitleştirici bir varsayım kullanarak işçiler tarafından sergilenen gerçek ekserji şu şekilde gösterilir:

Sermaye fonksiyonu da şu şekilde düzenlenir:

Denklem endüstri tarafından tüketilen toplam enerji miktarını göstermektedir. Son olarak ekserji verimliliğinin nasıl hesaplanacağı problemi var. Çok detaya girmeden basitçe çok sayıda endüstriyel süreç için ekserji verimliliği hesaplanıp ardından toplam verimlilik elde edilmektedir. Yukarıdaki fonksiyonu düzenlersek şu hale gelir:

Fark edebileceğiniz gibi birkaç farklı form var. Aşağıda birazdan bunlardan ikincisini kullanacağız.

Son kısım, GDP’nin (Q) tanımlanmasıdır. Fonksiyondaki üretim girdileri ekserji olduğu için çıktının da ekserji olması gerekiyor. Yani GDP, kullanışlı iş ile ölçülmeli. Dolayısıyla Q’nun iki bileşeni vardır. İlki GDP’yi üretmek için kullanılan total enerji. İkincisi de ekserjinin kullanışlı işe çevrilme verimliliğidir. Matematiksel olarak bunlar şu şekilde gösterilir:

Enerji-temelli Cobb-Douglas üretim fonksiyonunu elde etmeyi bitirdik. Yukarıda L(E) ve K(E) için elde ettiğimiz fonksiyonları bir araya getirirsek matematiksel olarak bunu şu şekilde gösteririz:

Fark edebileceğiniz gibi tekrar α ve β katsayılarının ne olacağını problemine dönmemiz gerekiyor. Fonksiyonu biraz değiştirirsek şunu elde ederiz:

Bunun elde etmek için öncelikle zaman notasyonunu attık. C’yi ise (E_X^L)^ß ifadesinin yerine koyduk. Yukarıdaki neoklasik iktisatçıların kullandığı CDPF’ye bakarsanız eğer şunu fark edeceksiniz. Toplam faktör verimliliği gerçekte ekserjinin üretime yaptığı katkıyı ifade etmektedir. Matematiksel olarak:

Toplam faktör verimliliği, neoklasik iktisatçıların düşündüğü gibi bir artık (residual) değil, üretim fonksiyonlarının, enerjinin rolünü hesaba katmaması nedeniyle, gerçeklerden kopuk bir şekilde tasarlanmasının ürünüdür.

Yukarıdaki enerji-temelli CDPF, aynı zamanda, standart CDPF’nin empirik tutarsızlıklara yol açan katsayı problemlerinden birini de açıklamaktadır. Sermayenin ekserji katkısı, emeğinkinden çok daha büyük olmasına rağmen neoklasik iktisatçılar emeğin katsayını (üçte iki), sermayeninkinden (üçte bir) çok daha büyük olarak hesaplamaktadırlar. Bunun sebeplerine ve yol açtığı empirik tutarsızlıklara başka bir yazıda daha detaylı değinebiliriz fakat basitçe neoklasik CDPF bir cebirsel oyundan ibarettir (Shaikh, 1974). Dolayısıyla katsayıları empirik tutarlılığı olacak şekilde belirlemeliyiz. Matematiksel olarak şu şekilde:

İlerleyen zamanlarda bu konuda daha fazla post yayınlayacağım. Buradaki amacımız sadece toplam faktör verimliliğinin ne olduğunu cevaplandırmaktı. Bu noktaya kadar okuduysanız eğer şu yazıyı da okumanızı tavsiye ediyorum.

Referanslar

Ayres, R. U. & Warr, B. The Economic Growth Engine: How Energy and Work Drive Material Prosperity. (Edward Elgar Publishing, 2010)

Keen, S., Ayres, R. U. & Standish, R. A note on the role of energy in production. Ecol. Econ. 157, 40–46 (2019).

Shaikh, A., 1974. Laws of production and Laws of algebra: the humbug production function. Rev. Econ. Stat. 56 (1), 115–120.