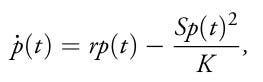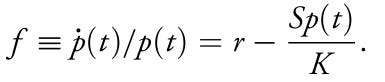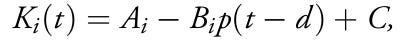Devletsiz Toplumlarda Nüfus Dinamikleri: Adaptif Kapasite Ödünleşim Modeli

Devletsiz toplumlar nasıl çöker?

Devletler ilk ortaya çıkışlarından itibaren insan popülasyonları için taşıma kapasitesini etkileyen önemli faktörlerden biri haline gelmiştir. Daha önceki bir yazıda tarım devletlerinin insan popülasyon dinamiklerini nasıl etkilediğini incelemiştik. Buna karşın devletsiz toplumlarda popülasyon dinamikleri nüfus ve taşıma kapasitesini belirleyen yenilenebilir doğal kaynaklar arasındaki ilişkiye dayanır. Bu yüzden Paskalya Adası yazımızda ele aldığımız gibi devlet öncesi nüfus dinamikleri Lotka-Volterra modelinin insan popülasyonları için değiştirilmiş versiyonları ile açıklanır.

Daha önce de vurguladığımız gibi insan popülasyonları için yerel düzeyde en yaygın davranış biçimi salınımdır. Başka bir yazıda açıkladığımız gibi dinamik sistemlerin aşma ve çöküş veya salınım davranışını sergileyebilmesi için gerekli koşul modelin en az iki stoktan oluşmasıdır. Bununla birlikte orada bahsetmediğimiz daha temel bir koşul bulunmaktadır. Dinamik sistemlerin salınımı için gerekli asıl yapısal unsur negatif geri bildirim döngülerinin zaman gecikmesi (time lags) ile işlemesidir. Dolayısıyla tek stoklu fakat negatif geri bildirim döngüsünün bir zaman gecikmesi ile işlediği sistemler de salınım davranışını sergileyebilir.

Tekrar insan popülasyon dinamiklerine dönecek olursak antropolojik bulgular salınım davranışının avcı-toplayıcı ve erken neolitik toplumlar için de yaygın olabileceğini göstermektedir. (Shennan ve ark., 2013) orta-Holosen Avrupası’nda erken tarım toplumlarının nüfus dinamiklerini incelemektedir. Çalışma, Avrupa kıtasında inceledikleri 12 bölgenin 10’unda tarıma geçişin ardından nüfus yoğunluklarında sıfır hipotezi (null model) olarak belirlenen üstel büyüme modeline kıyasla istatistiksel olarak anlamlı bir yükseliş ve düşüş döngülerinin varlığını tespit etmiştir.

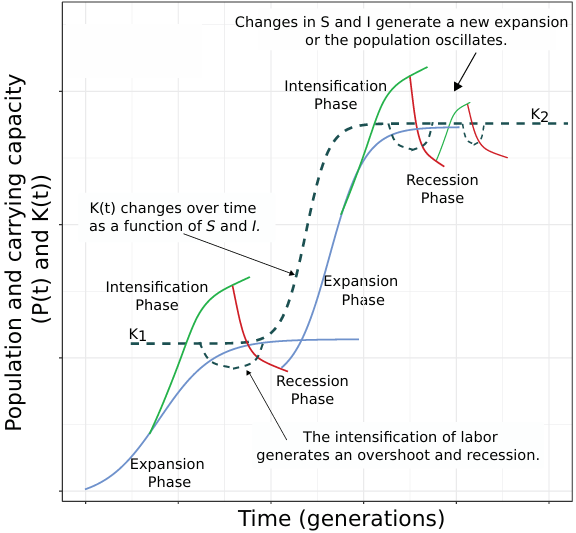
Bölgesel ve kısa dönemli dinamiklerden farklı olarak insan popülasyonlarının kıtasal/küresel ve uzun dönemli dinamikleri üstel büyüme olmuştur. (Goldewijk ve ark., 2010) küresel olarak Holosen boyunca insan popülasyonundaki artış oranını yıllık %0.04 olarak tahmin etmektedir. Büyüme oranı küçük gibi gelebilir fakat popülasyonlar için bu üstel büyüme anlamına gelmektedir. İnsan popülasyon dinamiklerine ilişkin bu iki bulguyu açıklayan bir referans modeli aşağıdaki grafikte görebilirsiniz:

Model özünde bir lojistik büyüme modeli fakat standart versiyonlarından farklı olarak taşıma kapasitesi zaman içerisinde değişebilmekte. Taşıma kapasitesini şu fonksiyonla göstermek mümkündür:

K(t) = f(X_e, L, S, I)

X_e ekosisteminin üretkenliğini ifade eder. L, doğal kaynak ekstraksiyonuna ayrılan emeği. S, üretimin sosyal organizasyonunu ve I, fiziksel altyapıyı ifade eder. Ekosistemin üretkenliği iklim değişikliği tarafından da etkilenebilir fakat taşıma kapasitesindeki değişim uzun dönemli olarak S ve I tarafından belirlenir. (Palmisano ve ark., 2021) insan toplumların karmaşıklaşmasıyla birlikte orta Holosen’den itibaren iklim ve demografik trendlerin birbirinden ayrıştığını raporlamaktadır. Bunun anlamı popülasyon dinamiklerinin dışsal iklim şokları yerine giderek daha çok içsel mekanizmalar tarafından belirlendiğidir.

Modelin en önemli varsayımlarından biri S ve I’nın patika bağımlılığı azalan getiriler sergilemesidir. Bunun anlamı popülasyonun taşıma kapasitesine ulaştığında pürüzsüz bir şekilde yeni S ve I biçimlerini geliştiremeyeceği ve benimsemeyeceğidir. Bu dönüm noktalarında uzun dönemli S ve I dinamikleri yerine Paskalya Adası’nda olduğu gibi klasik yenilenebilir kaynak dinamikleri baskın hale gelir. Artan nüfus baskısı altında toplum kaynak ekstraksiyonu yoğunlaştırarak üretimi arttırmak ve bunun sonucu olarak taşıma kapasitesini aşındırarak popülasyonu çöküşe daha açık hale getirmek arasında bir ödünleşimle karşılaşır.

Matematiksel Model

Bu kısımda yukarıdaki davranış biçimini sergileyecek bir matematiksel model yaratacağız. Yapmamız gereken şey basitçe taşıma kapasitesinin sabit olmadığı bir lojistik büyüme modeli yazmak.

Lojistik büyüme modelini şu şekildedir:

Denklemdeki ilk bileşen popülasyonun üstel büyüme eğilimini gösterir. S, sosyal organizasyonun maliyetini ölçer, 0 < S ≤ 1. K taşıma kapasitesidir.

Literatürdeki modeller taşıma kapasitesini arttıran inovasyonların nüfus baskısına bağlı olduğunu ileri sürdüğü için popülasyon baskısını tanımlayacak bir denklem yazmamız gerekiyor:

f, ortalama kişi başı uyumu (fitness) ifade eder. Modelde popülasyon baskısı belirli bir eşiği geçtiğinde inovasyonun teşvik edildiği varsayılmaktadır.

Son olarak taşıma kapasitesi şu denklemle gösterilir:

A_i, altyapının kaynak ekstraksiyonu üzerindeki etkisini ifade eder. C, ekosistemin üretkenliğini ifade eder. B_i, kaynakların üretkenliği ve nüfus yoğunluğu arasındaki ilişkiyi ifade eder. (t – d), popülasyonun kaynaklar üzerindeki etkisinin zaman gecikmesine tâbi olduğunu ifade eder.

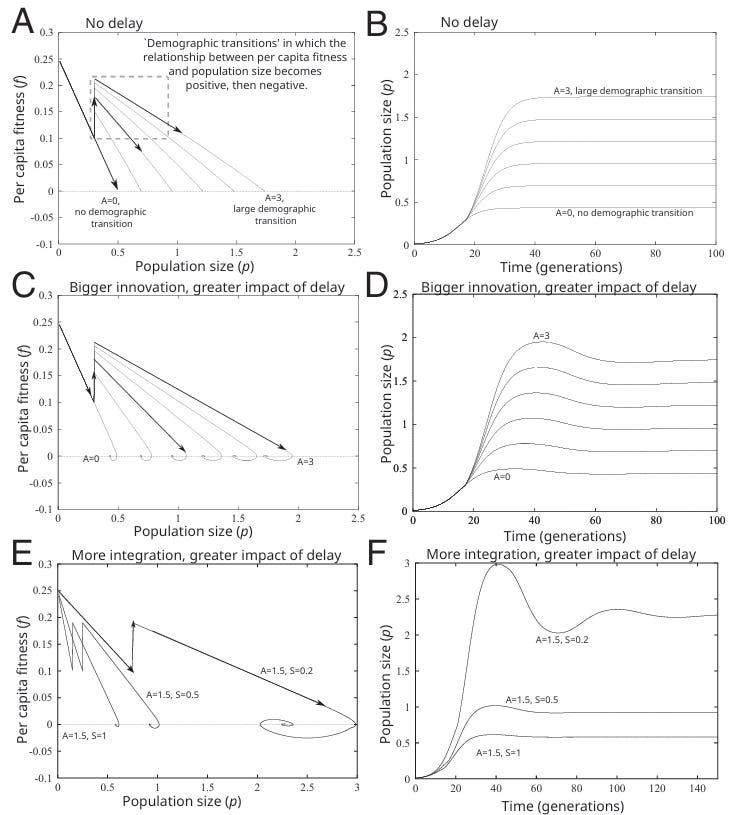
Modelin davranışını aşağıdaki grafiklerde görebilirsiniz. B, C ve r sabit tutulmaktadır. Model, A, S ve d’deki değişimlerin popülasyonun davranışını nasıl etkilediğini göstermektedir.

En üstteki iki grafikte (A ve B) popülasyon baskısı belirli bir kritik eşiği geçtiğinde popülasyon yeni bir üretim biçimine geçmektedir ve taşıma kapasitesini arttırmaktadır. İnovasyon ne kadar büyük olursa popülasyonun nihai olarak ulaşacağı büyüklük de o kadar yüksek olmaktadır. Fakat inovasyon, ekosistem üzerinde gecikmeli bir etkiye sahip olmadığı için popülasyon salınım davranışı sergilemez. Hemen altttaki iki grafikte (C ve D), zaman gecikmesi modele dahil edilmektedir. İnovasyon ne kadar büyükse zaman gecikmesinin etkisi de o kadar artmaktadır ve popülasyon daha şiddetli bir salınım sergilemektedir. En alttaki iki grafikte (E ve F) inovasyon sabit tutulmakta fakat S değişmektedir. S, popülasyon üzerindeki negatif geri bildirim döngüsünü belirlediği için bu değişkeni küçültmek popülasyonu daha büyük bir denge büyüklüğüne ulaştırmaktadır fakat aynı zamanda gecikmenin etkisini de arttırmaktadır.

Özetle, adaptif kapasite ödünleşim modeli insan popülasyonlarındaki uzun dönemli üstel büyümenin ve salınımların aynı sürecin ürünü olduklarını ileri sürer. Doğal kaynak ekstraksiyonundaki inovasyonlar uzun vadede popülasyondaki büyümenin motoru olarak işlev görmektedir. Fakat kısa vadede adaptif kapasiteyi arttıran aynı inovasyonlar sebep oldukları ekolojik transformasyonlar aracılığıyla nüfus yoğunluğuna bağlı negatif geri bildirim döngülerinde gecikmeler yaratırlar. Bu gecikmelerin nihai sonucu da popülasyon salınımlarıdır.

Referanslar

Freeman, J., Mauldin, R. P., Whisenhunt, M., Hard, R. J. & Anderies, J. M. 2023. Repeated long-term population growth overshoots and recessions among hunter-gatherers. The Holocene 7, 09596836231183072.

Freeman, J. et al. 2024. The long-term expansion and recession of human populations. Proc. Natl Acad. Sci. USA 121, e2312207121.

Palmisano, A., Lawrence, D., de Gruchy, M. W., Bevan, A. & Shennan, S. 2021. Holocene regional population dynamics and climatic trends in the Near East: A frst comparison using archaeo-demographic proxies. Quat. Sci. Rev. 252, 106739.

Klein Goldewijk K, Beusen A, Janssen P. 2010. Long-term dynamic modeling of global population and built-up area in a spatially explicit way: HYDE 3.1. Holocene 20:565–73.

S. Shennan et al., 2013. Regional population collapse followed initial agriculture booms in mid-Holocene Europe. Nat. Commun. 4, 2486.