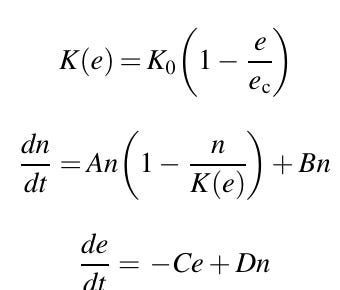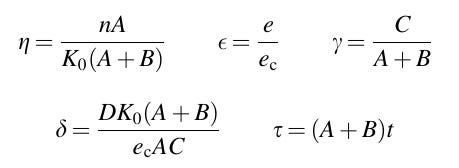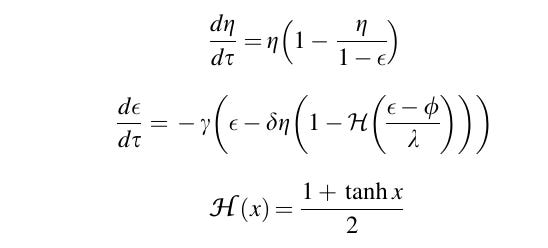Antroposenin Astrobiyolojisi

Teknolojik Medeniyetlerde Ekolojik Sürdürülebilirlik

Antroposen, Dünya gezegeninde evrimleşen fazlaca zeki bir kuyruksuz maymun türü tarafından sebep olunan bir jeolojik olaydır. Gezegen tarihi boyunca birden fazla kez başka canlı türleri tarafından sebep olunan olaylar (örneğin büyük oksidasyon olayı) tarafından dönüşüme uğradı. Antroposenin ayırt edici yanı gezegenin doğal kaynaklarını hasat eden bir canlı türünün aktivitelerinin dünya sistemi üzerindeki etkilerinden oluşmasıdır. Evrendeki başka gezegenlerde evrimleşmiş kaynak hasat eden canlı türleri de kendi antroposenlerini yaratabilir mi yoksa antroposen dünya gezegenine özgü bir olay mı? Antroposen teknolojik medeniyet inşa etmek için kaynak hasat eden canlı türlerini barındıran gezegenlerin genel bir özelliği olabilir mi? Bu yazıda bunun gibi sorulara cevap vermek için geliştirilmiş bir modeli inceleyeceğiz.

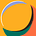
Modelleri oluştururken doğal kaynakların sınırsız olduğunu varsayarak uzaylı medeniyetin popülasyonu ve gezegensel sistemler arasındaki dinamiklere odaklanacağız. Canlı popülasyonundan bahsettiğimiz için dünyadaki canlılar gibi üstel büyüme eğilimine sahip olacaktır fakat aynı zamanda çeşitli aktivitelerinin gezegensel sistemler üzerindeki etkileri nedeniyle popülasyon büyümesi bazı biyofiziksel sınırlara tabi olacaktır. Dolayısıyla başlangıç olarak basit bir lojistik büyüme modeli kullanabiliriz. Denklemler şu şekildedir:

Ortadaki denklem popülasyon için lojistik büyüme denklemidir. K(e) taşıma kapasitesini ifade eder. En alttaki denklem çevrenin (e) doğal iyileşme oranına (C) sahip olduğunu söylemektedir. e = 0 olduğunda çevre en sağlıklı durumdadır. e_c çevre için kritik değeri ifade eder öyle ki e = e_c olduğunda K(e) = 0’dır. Bn, doğal kaynakların tüketilmesinin popülasyon büyümesi üzerindeki etkisini ifade eder. Dn, doğal kaynakların çıkarılması ve tüketilmesinden kaynaklanan çevresel etkileri ifade eder. Modelin değişkenlerini kullanarak bazı boyutsuz parametreler tanımlanmaktadır. Bunların ne ifade ettiğine değineceğiz.

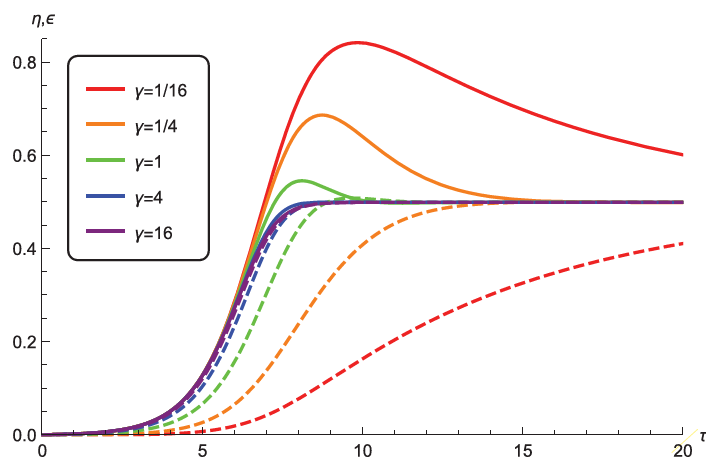
Aşağıdaki grafikte belirli bir δ (forcing) değeri için modelin davranışı görülmektedir. δ, çevrenin iyileşme oranıyla normalize edilmiş doğal kaynak kullanımının sebep olduğu zararı ifade eder. γ, popülasyonun büyüme oranıyla normalize edilmiş çevrenin iyileşme oranını ifade eder. Bu parametre çevrenin hassasiyetini gösterir. η, maksimum taşıma kapasitesi ile normalize edilmiş popülasyonu ifade eder. ϵ, taşıma kapasitesini sıfır olduğu kritik değere göre normalize edilmiş çevresel durumu ifade eder.

Grafikte görüldüğü gibi popülasyon her zaman bir dengeye doğru gitmektedir fakat çevrenin hassasiyet düzeyi dengeye nasıl ulaşacağını belirlemektedir. Yüksek hassasiyet seviyelerinde popülasyon taşıma kapasitesini aşmadan ve dolayısıyla salınım göstermeden dengeye ulaşır. Düşük hassasiyet seviyelerinde ise popülasyon taşıma kapasitesini aşar ve salınım davranışı sergileyerek dengeye ulaşır. Bunun sebebi basitçe düşük hassasiyetin çevrenin tepkisi açısından daha büyük bir zaman gecikmesi ifade etmesidir.

İlk modelde doğal kaynaklar arasında bir ayrım yapmadan tüketimlerinin belirli bir çevresel etkiye sahip olduğunu varsaydık. Fakat doğal kaynaklar daha yüksek ya da daha düşük çevresel etkilere sahip olabilirler. Örneğin, dünya gezegenindeki antroposonin sorumlusu teknolojik medeniyet yüksek çevresel etkiye sahip fosil hidrokarbonlardan, daha düşük çevresel etkiye sahip olacağına inandığı güneş ve rüzgardan üretilen elektrik enerjisine geçmeye çalışmaktadır.

Enerji/kaynak dönüşümünü modellemek için çevrenin belirli bir kritik değere (e/e_c = Φ) ulaştığında dönüşümün başladığını varsayacağız. Denklemleri aşağıda görebilirsiniz. λ, enerji/kaynak dönüşümünün hızını ifade etmektedir. Φ, değeri teknolojik medeniyetin basiretini (foresight) ölçmektedir ve daha düşük değerler, daha büyük bir basirete işaret etmektedir.

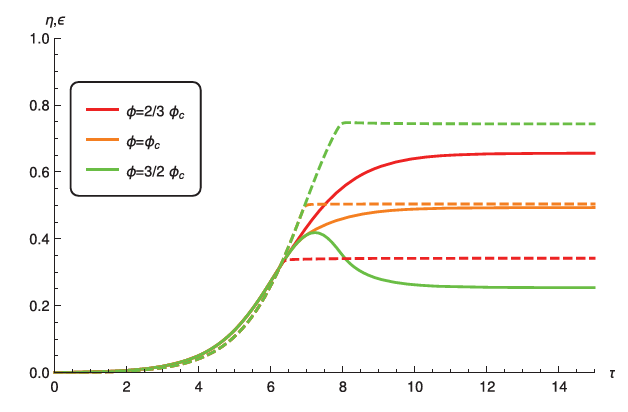
Aşağıdaki grafikte farklı basiret değerleri için sistemin davranışı görülebilir:

Teknolojik medeniyetin basiretinin yüksek olduğu durumda popülasyon salınım davranışını sergilemeden dengeye ulaşmaktadır fakat düşük olduğu durumda popülasyon taşıma kapasitesi aşar ve popülasyon çöktükten sonra dengeye ulaşır.

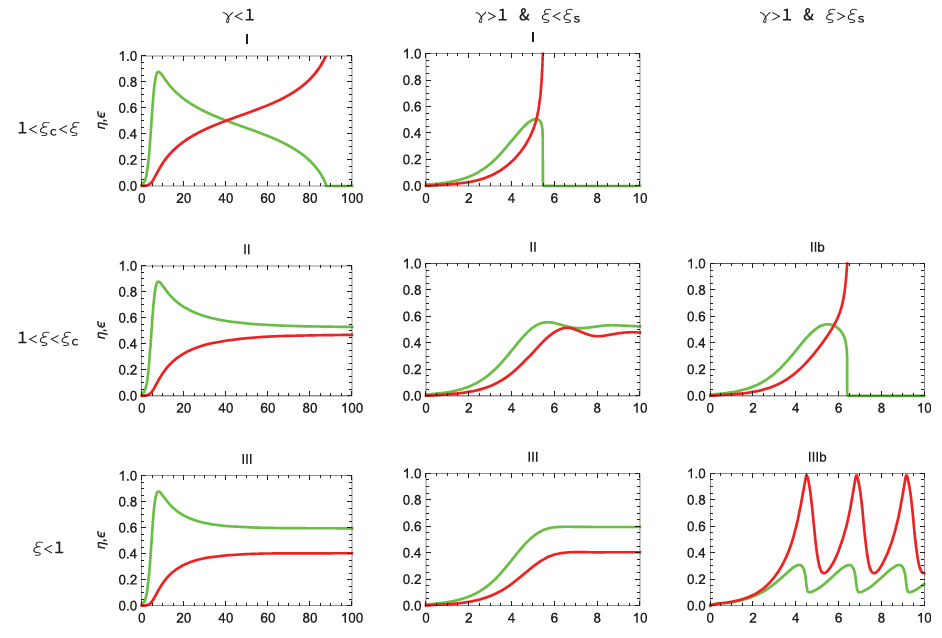
Önceki iki modelde çevrenin tepkisinin lineer olduğunu varsaydık fakat gezegensel sistemler sıklıkla lineer olmayan davranışlar sergiler. Örneğin, dünya gezegeninde iklim sistemi birden fazla devrilme noktasına sahiptir ve bunlar aşıldığında ani (abrupt) iklim değişikliği senaryoları gerçek olabilir. Çevresel oto-regülasyonu modellemek için ϵ > 1/ξ olduğu durumlarda kontrolsüz çevresel yıkımın ortaya çıktığını varsayacağız. ξ, çevrenin kırılganlığını (fragility) ifade eder. Modele daha fazla parametre dahil ettikçe sistemin davranış çeşitliliği de artmaktadır. Aşağıdaki grafikte farklı parametre değerleri için popülasyon (yeşil) ve çevrenin (kırmızı) davranışını görebilirsiniz. ξ_c, dengenin var olması için gerekli kritik kırılganlığı ve ξ_s, bu dengelerin stabil olması için gerekli kritik kırılganlığı ifade eder. ξ > ξ_c olduğu durumlarda sistem aşırı kırılgandır, kendi kendini regüle edemez ve taşıma kapasitesi yeterince hızlı düşmediği için çevre, popülasyon tarafından ani bozulmaya uğrar.

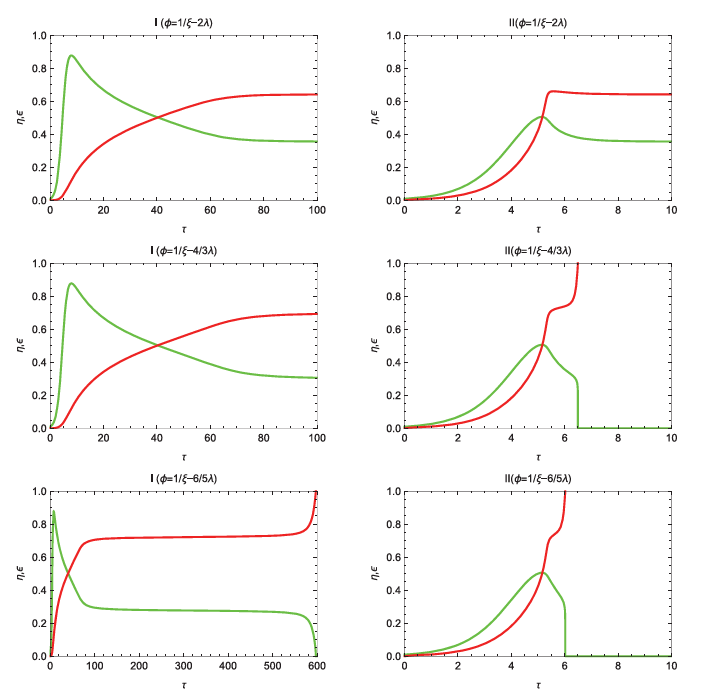
Son olarak, modele enerji/kaynak dönüşümünü de dahil edeceğiz. Bunun sonuçlarını aşağıdaki grafikte görebilirsiniz. Buradaki tüm senaryolarda sistemin aşırı kırılgan olduğu varsayılmaktadır. Yine birden fazla farklı davranış biçimi göze çarpmaktadır. Sol taraftaki grafiklerde çevrenin hassasiyeti düşük ( γ << 1) ve sağ taraftakilerde yüksektir ( γ >> 1). Aynı zamanda en üstteki grafiklerde medeniyetin basireti yüksektir ve en alttaki grafiklerde basireti düşüktür.

Fermi Paradoksu

Buradaki model ve simülasyonlar Fermi paradoksu açısından bir öneme sahiptir. Çünkü Fermi paradoksunun çıkış noktası olan Drake denkleminin son faktörü teknolojik medeniyetlerin yaşam ömrüdür (L). Daha ileri simülasyonlar L’nin teorik olarak tahmin edilmesine olanak sağlayabilir. Eğer teknolojik medeniyetlerin yaşam ömrünün aşırı kısa olduğunu ortaya çıkarsa bu Fermi paradoksu için de bir açıklama sunabilir. Kendilerinin sebep oldukları antroposenler teknolojik medeniyetler için büyük filtrelerden birini teşkil ediyor olabilir.

Referanslar

Frank, A., Carroll-Nellenback, J., Alberti, M. & Kleidon, A. The Anthropocene Generalized: Evolution of Exo-Civilizations and Their Planetary Feedback. Astrobiology 18, 503–517 (2018).